angles worksheet with answers pdf

Angles Worksheet with Answers PDF⁚ A Comprehensive Guide

This comprehensive guide provides a detailed overview of angles worksheets with answers in PDF format. It covers various aspects of angle concepts, including types of angles, angle properties, angle relationships, worksheet examples, finding missing angles, practice problems, solutions and explanations, verifying answers, applications of angles, tips for solving angles worksheets, and a conclusion. These worksheets are valuable resources for teachers, parents, and students who want to enhance their understanding of angles and geometry.

Introduction

Angles are fundamental concepts in geometry that play a crucial role in understanding shapes, measurements, and spatial relationships. Angles worksheets with answers provide a structured and engaging way to learn and practice these concepts. These worksheets typically feature a variety of problems, ranging from basic angle identification and measurement to more complex calculations involving angle relationships and geometric figures. The inclusion of answers allows students to check their work, identify areas where they need further practice, and gain confidence in their understanding of angles.

Angles worksheets are valuable learning tools for students of all ages. They can be used in classrooms, at home, or for self-study. They offer a hands-on approach to learning geometry, encouraging students to visualize, analyze, and solve problems involving angles. The use of PDFs allows for easy access, printing, and distribution, making these worksheets convenient for both teachers and students.

This guide will delve into the various aspects of angles worksheets with answers in PDF format, providing a comprehensive overview of the concepts, examples, and applications. Whether you’re a student looking to master angles or an educator seeking effective teaching materials, this guide will serve as a valuable resource for your learning journey.

Types of Angles

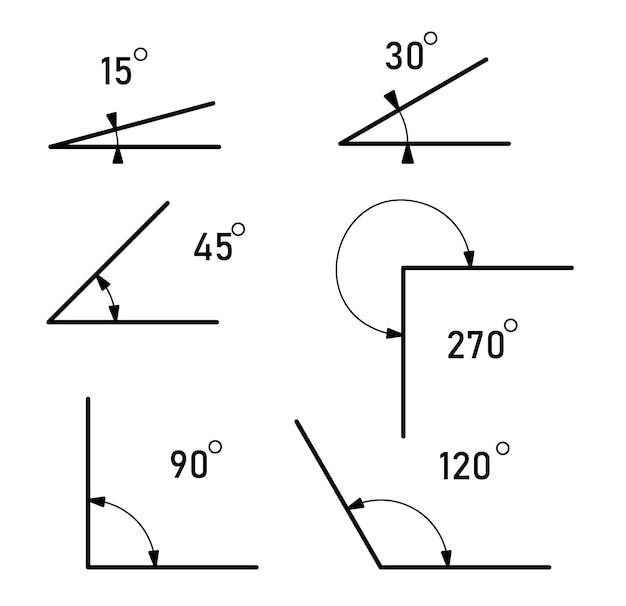
Angles are classified based on their measures, and understanding these classifications is essential for solving problems involving angles. The most common types of angles include⁚

• Acute Angle⁚ An acute angle measures less than 90 degrees. It is a sharp angle, often found in triangles and other geometric shapes.
• Right Angle⁚ A right angle measures exactly 90 degrees. It is represented by a small square symbol at the vertex of the angle. Right angles are crucial in constructing squares, rectangles, and other geometric figures.
• Obtuse Angle⁚ An obtuse angle measures greater than 90 degrees but less than 180 degrees. It is a wider angle than a right angle, often found in polygons with more than four sides.
• Straight Angle⁚ A straight angle measures exactly 180 degrees. It forms a straight line, and it is often used to represent a complete rotation of 180 degrees.
• Reflex Angle⁚ A reflex angle measures greater than 180 degrees but less than 360 degrees. It is an angle that makes more than a half-turn.
• Full Angle⁚ A full angle measures 360 degrees. It represents a complete rotation around a point.

Angles worksheets often include problems that require students to identify and classify different types of angles based on their measures. These exercises help students develop their understanding of angle terminology and their ability to visualize and compare angles.

Angle Properties

Angles possess several fundamental properties that govern their behavior and relationships within geometric figures. Understanding these properties is crucial for solving angle problems and applying angle concepts to real-world scenarios. Some key angle properties include⁚

• Angle Addition Postulate⁚ This postulate states that the measure of an angle formed by two adjacent angles is equal to the sum of the measures of the two adjacent angles. For example, if angle A and angle B are adjacent angles, then the measure of angle C (formed by A and B) is equal to the measure of angle A plus the measure of angle B.
• Angle Subtraction Property⁚ This property states that the difference between the measures of two angles is equal to the measure of the angle formed by subtracting the smaller angle from the larger angle. For example, if angle A is larger than angle B, then the measure of angle C (formed by subtracting angle B from angle A) is equal to the measure of angle A minus the measure of angle B.
• Vertical Angles Theorem⁚ This theorem states that vertical angles (angles formed by the intersection of two lines) are congruent, meaning they have the same measure. This property is frequently used to solve problems involving angles formed by intersecting lines.
• Angle Bisector Property⁚ An angle bisector divides an angle into two congruent angles. This property is useful for finding the measures of angles that are bisected or for determining the relationship between bisected angles.

Angles worksheets often incorporate problems that require students to apply these angle properties to calculate unknown angle measures or prove angle relationships. These exercises help students develop their problem-solving skills and their understanding of angle relationships within geometric figures.

Angle Relationships

Angles exhibit various relationships with one another, forming the foundation of geometric concepts and problem-solving techniques. These relationships are essential for understanding the properties of shapes, solving angle problems, and applying angle concepts to real-world applications. Some key angle relationships include⁚

• Complementary Angles⁚ Two angles are complementary if their measures add up to 90 degrees. This relationship is often used in right triangles, where the two acute angles are complementary.
• Supplementary Angles⁚ Two angles are supplementary if their measures add up to 180 degrees. This relationship is frequently encountered in linear pairs, where two angles form a straight line.
• Adjacent Angles⁚ Adjacent angles share a common vertex and a common side. They do not overlap, but they are next to each other. Understanding adjacent angles is crucial for applying the Angle Addition Postulate and solving angle problems involving combined angles.
• Vertical Angles⁚ As mentioned earlier, vertical angles are formed by the intersection of two lines and are congruent. This relationship is often used to solve problems involving intersecting lines and find unknown angle measures;
• Linear Pairs⁚ A linear pair consists of two adjacent angles that form a straight line. The measures of the two angles in a linear pair always add up to 180 degrees, making it a special case of supplementary angles.

Angles worksheets often incorporate problems that require students to identify and apply these angle relationships to solve problems involving unknown angles, prove geometric relationships, and understand the properties of shapes. These exercises help students develop their geometric reasoning skills and their understanding of angle relationships within geometric figures.

Worksheet Examples

Angles worksheets provide a structured platform for students to practice and solidify their understanding of angles and their relationships. These worksheets typically include a variety of problem types, ranging from basic angle identification and measurement to more complex problems involving geometric proofs and applications. Here are some examples of common angle worksheet problems⁚

• Angle Identification⁚ Students may be asked to identify different types of angles, such as acute, obtuse, right, straight, and reflex angles. They may also be required to classify angles based on their position within a given figure, such as vertical angles, adjacent angles, or linear pairs;
• Angle Measurement⁚ Worksheets often include problems requiring students to calculate the measure of unknown angles using given information and angle relationships. This may involve applying the Angle Addition Postulate, using complementary or supplementary angles, or working with vertical angles.
• Missing Angle Problems⁚ Students may be presented with diagrams showing angles with unknown measures and asked to determine those measures using their knowledge of angle relationships and properties of geometric figures. These problems often involve solving equations or applying logical reasoning.
• Geometric Proofs⁚ Some worksheets may include problems requiring students to prove geometric relationships involving angles using formal proofs. This involves applying deductive reasoning and angle properties to justify conclusions.
• Real-World Applications⁚ Angles worksheets can also incorporate problems that demonstrate the practical applications of angle concepts in real-world scenarios. These problems may involve calculating angles in construction, navigation, or other fields.

By working through a variety of these problems, students gain confidence in their ability to identify, measure, and manipulate angles, strengthening their foundation in geometry and preparing them for more advanced mathematical concepts.

Finding Missing Angles

A significant portion of angles worksheets focuses on finding missing angles within various geometric figures. These problems challenge students to apply their knowledge of angle relationships and properties to solve for unknown angle measures. Here are some common techniques employed in finding missing angles⁚

• Angle Addition Postulate⁚ This postulate states that the measure of a larger angle is equal to the sum of the measures of its smaller adjacent angles. Students can use this postulate to set up equations and solve for unknown angles.
• Complementary and Supplementary Angles⁚ Complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees. By recognizing these relationships, students can use given angle measures to determine the measure of an unknown angle.
• Vertical Angles⁚ Vertical angles are opposite angles formed by the intersection of two lines. They are always congruent (equal in measure). Students can use this property to determine the measure of an unknown angle if its vertical angle is known.
• Linear Pairs⁚ A linear pair consists of two adjacent angles that form a straight line. The sum of their measures is always 180 degrees. By applying this property, students can find the measure of an unknown angle if its linear pair is known.
• Triangle Angle Sum Theorem⁚ The sum of the interior angles of any triangle is always 180 degrees. This theorem can be used to find missing angles in triangles, especially when two angles are known.

Angles worksheets with answers provide students with a platform to practice these techniques and develop their problem-solving skills in geometry.

Practice Problems

Angles worksheets with answers often include a variety of practice problems designed to reinforce the concepts learned and help students develop their problem-solving skills. These problems can range in difficulty from simple angle identification to more complex calculations involving multiple angle relationships. Here are some common types of practice problems found in angles worksheets⁚

• Identifying Angle Types⁚ Students may be asked to identify different types of angles, such as acute, obtuse, right, straight, and reflex angles, based on their measurements or diagrams.
• Finding Missing Angle Measures⁚ These problems require students to apply their knowledge of angle relationships, such as complementary, supplementary, vertical, and linear pairs, to calculate the measure of an unknown angle.
• Solving for Unknown Angles in Geometric Figures⁚ Students may be presented with diagrams of triangles, quadrilaterals, or other polygons, and asked to find the measure of missing angles using the properties of these figures.
• Word Problems⁚ These problems involve real-world scenarios where students need to identify angles and apply their knowledge of angle relationships to solve for unknown values. For example, a word problem might ask students to find the angle of elevation of a ladder against a wall.
• Multiple Choice Questions⁚ Angles worksheets may include multiple-choice questions where students need to choose the correct answer based on their understanding of angle concepts and calculations.

By working through these practice problems, students gain confidence in their ability to work with angles and develop a deeper understanding of geometric principles.

Solutions and Explanations

The inclusion of solutions and explanations is a crucial aspect of angles worksheets with answers. These elements provide students with a clear understanding of how to approach and solve problems involving angles. Here’s how solutions and explanations enhance the learning experience⁚

• Verification and Learning⁚ Solutions allow students to check their answers and identify any mistakes they may have made. This self-assessment process is essential for reinforcing learning and promoting independent study.
• Step-by-Step Guidance⁚ Explanations provide students with a detailed breakdown of the solution process. This step-by-step guidance clarifies the logic behind each calculation and helps students understand the underlying concepts.
• Problem-Solving Strategies⁚ Solutions and explanations often demonstrate different problem-solving strategies, exposing students to multiple approaches to tackle similar problems. This fosters flexibility and adaptability in their thinking.
• Conceptual Clarity⁚ Explanations often connect the solution to the relevant angle properties and theorems, solidifying students’ understanding of the underlying geometric principles. This deeper understanding helps them apply the concepts to new situations.
• Active Learning⁚ Solutions and explanations encourage active learning by prompting students to analyze the solution process, identify their own errors, and apply the learned strategies to new problems. This proactive engagement enhances learning and retention.

By providing comprehensive solutions and clear explanations, angles worksheets with answers create an effective learning environment that supports student understanding, problem-solving, and critical thinking skills.

Verifying Answers

Verifying answers is an integral part of the learning process when working with angles worksheets. It allows students to assess their understanding and identify any areas where they might need further review or clarification. Here’s how verifying answers contributes to effective learning⁚

• Self-Assessment⁚ Verifying answers encourages students to take ownership of their learning by evaluating their own work. This self-assessment process promotes active engagement and helps them identify their strengths and weaknesses.
• Error Correction⁚ By comparing their answers to the provided solutions, students can pinpoint any mistakes they might have made. This process allows them to correct errors and understand where they went wrong, preventing future repetitions.
• Strengthening Concepts⁚ The process of verifying answers reinforces the understanding of angle properties, relationships, and theorems. It encourages students to recall and apply these concepts to solve problems.
• Building Confidence⁚ Successfully verifying answers boosts students’ confidence in their abilities. It encourages them to tackle more challenging problems and reinforces their positive learning experiences.
• Identifying Gaps⁚ If students find that they consistently make errors in a particular area, it highlights a potential gap in their understanding. This realization allows them to focus their learning efforts on specific areas that require further attention.

Verifying answers fosters a cycle of self-evaluation, error correction, and continuous learning. It empowers students to take control of their learning journey and achieve a deeper understanding of angles and geometry.

Applications of Angles

Angles are fundamental concepts in geometry, and their applications extend far beyond the realm of textbooks and worksheets. They play a crucial role in various fields, demonstrating their real-world relevance and practical utility. Here are some key applications of angles⁚

• Engineering and Architecture⁚ Angles are essential for structural design, ensuring stability and load distribution in buildings, bridges, and other structures. Engineers and architects use angles to calculate forces, stresses, and strains, ensuring the safety and efficiency of construction projects.
• Navigation and Surveying⁚ Angles are vital for navigation, allowing ships, aircraft, and spacecraft to determine their position and course. Surveyors use angles to measure distances, elevations, and land boundaries, creating precise maps and plans.
• Computer Graphics and Animation⁚ Angles are fundamental in computer graphics and animation. They define the perspective, rotation, and movement of objects in virtual environments, creating realistic and visually engaging experiences.
• Robotics and Automation⁚ Robots and automated systems rely heavily on angles for precise movements, positioning, and manipulation. Angle calculations enable robots to perform tasks with accuracy and efficiency in various industries, including manufacturing and healthcare.
• Astronomy and Space Exploration⁚ Angles are crucial for understanding celestial objects and their movements. Astronomers use angles to measure distances, sizes, and positions of stars, planets, and galaxies, expanding our knowledge of the universe.

These examples highlight the diverse applications of angles across various fields. From building structures to navigating the cosmos, angles play a critical role in shaping our world and advancing our understanding of it.